Genetic Equilibrium

Genetic Equilibrium Definition

Genetic equilibrium is a term used to describe a condition of static, or unchanging, allele frequencies in a population over time. Typically in a natural population the frequencies of alleles tend to shift as generations pass and different forces act on a population. This could be caused by many factors including natural selection, genetic drift, mutation and others which forcibly change the allele frequency. However, if a population is at genetic equilibrium these forces are absent or cancel each other out. The examples below show genetic equilibrium from a modeling context and in a natural context.

Examples of Genetic Equilibrium

Hardy-Weinberg Equilibrium

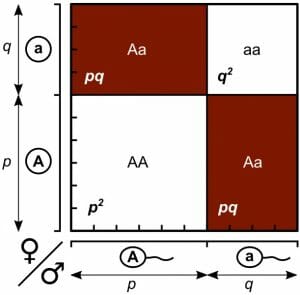
When modeling population dynamics, scientists often use the Hardy-Weinberg model. This equation takes the frequencies of the alleles in a population and multiplies them using the principles of the Punnett square to simulate the distribution of alleles during mating. A picture of this model can be seen below.

This diagram follows one gene, which has two alleles (A) and (a). The allele frequency of each allele is represented by the “p” and “q”. According to the Hardy-Weinberg model, these allele frequencies will not change from generation to generation without outside influences. In other words, a genetic equilibrium occurs in the absence of things like natural selection and genetic drift. If (A) and (a) are the only alleles in the system then the frequencies of (A) added to (a) must be 1. Therefore, in a system at genetic equilibrium, the frequency of the genotypes in the offspring can be estimated multiplying the allele frequencies. Homozygous dominant individuals (AA) can be estimated by p² or the frequency of (A) squared. The same is true of homozygous recessive individuals (aa); in genetic equilibrium they can be estimated by q². Heterozygous individuals can be estimated by 2pq. At genetic equilibrium the sum of all the genotypic frequencies for each gene is 1. In mathematical terms: p²+2pq+q²=1.

In the early 1900s, the science of inheritance was a new and exciting field. Gregor Mendel had shown in the 1800s that organisms carry two copies of each gene. These copies can come in different forms, or alleles. However, scientists were still grappling with the larger questions of how alleles change over time. One of the fundamental problems at the time was understanding how genes interacted with each other, especially dominant and recessive genes. It was assumed by some that the dominant allele would naturally increase in a population. This was disproven independently by several scientists using mathematics. However, only Hardy and Weinberg commonly get their name attached to the law. Genetic equilibrium in this idealized situation is commonly referred to as Hardy-Weinberg equilibrium.

Genetic Equilibrium due to Balancing Selection

In nature, things are never as perfect as the assumptions made in the Hardy-Weinberg model. This does not mean that genetic equilibrium cannot exist. In fact, it is easy to think up a scenario in which genetic equilibrium is maintained in the face of natural selection. The selection must simply be applied equally to the different allele present. In this way the allele frequency will be maintained and the population will remain at genetic equilibrium.

This can be demonstrated by a hypothetical group of animals. For our purposes we will consider a population of grasshoppers, with only two alleles for the gene that codes for their color. One allele codes for green: C_g. The C_b allele codes for brown. Homozygous individuals for either allele will be that color. However, in our hypothetical case, pretend that heterozygous individuals (C_gC_b) turn part green and part brown. A field is full of these grasshoppers, with equal parts of each type of grasshopper.

Now, a new predator is introduced to the field. A bird swoops over the field, picking off grasshoppers as it goes. The bird uses color vision to pick out its prey, and the solid green and brown grasshoppers are easily picked off. The heterozygous grasshoppers have a natural camouflage, and cannot be seen by the birds. Clearly, these varieties would be selected for over time. Eventually, this will change the distribution of genotypes. However, as long as the homozygotes are selected against equally the allele frequencies will not change. While organism are being eaten, the overall ratio of alleles will not change because the heterozygotes are being selected for and contain both alleles, preserving the ratio. Therefore genetic equilibrium is maintained even in the face of this balancing selection.

Random Genetic Equilibrium

There are a wide variety of forces which act upon population genetics. While Hardy-Weinberg assumes these forces are not at work, it is equally likely that they might cancel each other out. Hardy-Weinberg assumes that the population is not experiencing selection, mutation, or any immigration or emigration which would disrupt allele frequencies. Just as with the grasshoppers, it is easy to contrive a situation in which these forces could balance each other out and maintain the allele frequencies.

While a selection force might be actively trying to remove an allele from a population, mutation may keep it in the population. This is true of many genetic conditions created by non-functioning alleles. Selection naturally tries to reduce these mutated alleles, but the rate of mutation may keep the disease at some base level in a population. This would be a case of genetic equilibrium, caused by a confluence of several factors. It can also be seen how mutation could easily be replaced by a variety of other factors which could serve the same purpose.

Quiz

1. A scientist is observing a small population of armadillos. Over time, the allele frequencies of this small population shift around, but the scientist cannot pinpoint the cause of the change. It does not appear to be natural selection of any kind. Which of the following is a reason why the population is not at genetic equilibrium?
A. Genetic Drift
B. A new predator is shifting the alleles
C. The scientist is bad at measuring

2. A classmate of yours tries to argue that genetic equilibrium is proof that at least some populations don’t evolve. What do you tell them?
A. They are correct!
B. Evolution is a process over time, where equilibrium is just one point on that timeline
C. Equilibrium means that evolution is finished

3. There are 8 snails in a population. There are two white snails, six pink snails, and two red snails. The pink snails are the heterozygotes. Is this population at equilibrium?
A. Yes
B. No
C. Not enough info

References

• Hartwell, L. H., Hood, L., Goldberg, M. L., Reynolds, A. E., & Silver, L. M. (2011). Genetics: From Genes to Genomes. Boston: McGraw Hill.