Definition
Radial symmetry describes living and non-living forms; these forms can be equally divided into three or more sections that, when rotated through a center of rotation by more than 0° and less than 360°, exactly match each other in orientation and shape. Radial symmetry does not deal with mirror images but near-perfect matches, for example the five equidistant arms of a starfish that circle its central body and are of the same size and shape.

What is Radial Symmetry?
The definition of radial symmetry in animals, plants and other organisms concerns a complete or partial form that is the result of a series of anatomical sections that repeat on multiple planes. By turning each section on a rotational axis, they will rotate above 0° and under 360° to near-exactly match the next section. Furthermore, the environment that surrounds each repeated section must be the same.
Tentacles and petal formations are common radial symmetry examples, and the number of repetitions of the same anatomical structure within a 360° range of movement gives each organism, plant, or even molecular structure a name that tells us how many repetitions there are. The word actinomorphic refers specifically to radial symmetry – you may have heard of actinomorphic flowers. Actino is Greek for a ray; think of the rays of the sun coming from its core like the spokes of a bicycle wheel. Morphic refers to shape. The word tells us that something has a radial form, with every section between the spokes or rays representing a near-exact copy of the other sections.

A trimeric organism consists of three repeated anatomical structures, a tetrameric organism refers to four repeated structures, pentameric to five, hexameric to six, heptameric to seven, and octameric to eight. Organisms with any of these structures or higher fall under the group term of multimeric organisms. All are composed of equidistant and repetitive shapes. Radial symmetry can also correspond to part of an object. The petal arrangement of a flower can be multimeric while the leaves and roots are not. If you cut horizontally through an apple, you will seen an example of internal pentamerism in the star-shaped cross-section of the apple core. The intestines show radial symmetry, as do the muscular layers of blood vessels. A molar tooth when viewed from above exhibits radial symmetry.
In the field of biology, radial symmetry is nearly always approximate. If you compare two tentacles on the same animal they will not be exactly the same in form. When you look at the sliced open apple, not every seed pod is the same shape. Unlike architecture and man-made items, nature does not have to be exact.
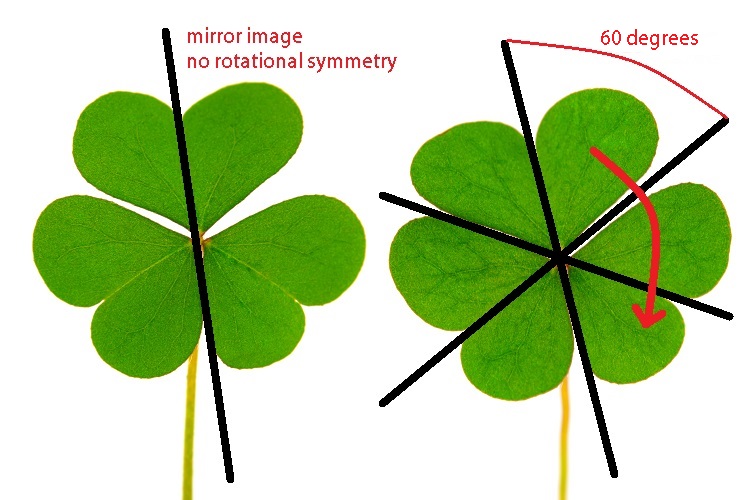
Radial or rotational symmetry is best explained visually. If you ignore the stem and place a three-leaf clover flat on a table – or draw one – with one leaf at the top and the two other leaves pointing slightly downwards, how many lines can you draw through it to produce a near-exact copy? First, we can draw a straight, vertical line through the middle of the top leaf. The result is two sections, both featuring half of the top leaf and one lower leaf. However, all we done is produce a bilateral symmetry example (below left).
The majority of organisms are bilaterally symmetrical, including us. If you draw a line through the center of our bodies, both halves feature an arm and a leg. However, these sections only match each other if one is folded over. In other words, these halves are mirror images.
Rotational symmetry does not deal with mirror images but depends on degrees of rotation where the various equal sections rotate to exactly match each other. Only by turning the left-hand side of the body a full circle – 360° – does the outline match. And as it has traveled the full circle, it is not the match of another section but has simply returned to its original position. This is not rotational symmetry.
If we go back to our three-leaf clover example (right-hand image), we can draw two more lines – a diagonal line that goes through the middle of the lower left-hand leaf and another going through the lower right-hand leaf. We have now divided the three leaves into six sections, each of which contain half a leaf. Where a single leaf is divided into two, there is a problem. They are mirror images of one other and if rotated by 60° do not have the same orientation. A single leaf is, therefore, bilaterally symmetrical. But the leaf group has more than one axis, and this is where the rotation part of rotational symmetry comes in.
In your mind’s eye or using the above image, rotate half a leaf, a set of two half leaves, or three half leaves until it exactly matches the position and shape of the next half leaf. You will need to rotate them 120°. The red arrow in the picture of the three-leaf clover radial symmetry example shows the degree of rotation. A complete circle is 360° and one third of this is 120° – this means the three-leaf clover has order-three rotation or 3-fold rotation, or is trimeric/trimerous.
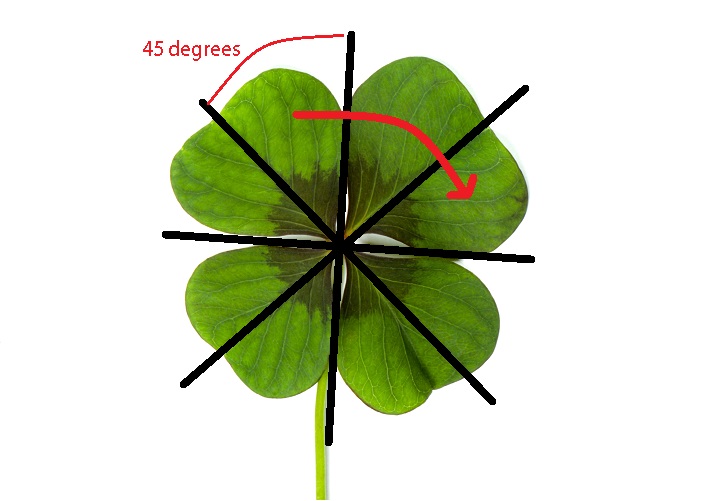
Now let us do the same with a four-leaf clover – drawing one will be necessary due to their rarity, and ignore the stem. Two planes have already been filled in by natural means – the lines of the central leaf veins that form a diagonal cross. We can add two straight lines that run between adjacent leaves.
With four planes – the natural X and the drawn or imagined cross – each 45° section can be rotated through 90° and exactly match the shape of the destination sector. A full 360° circle is composed of four 90° angles, so the four-leaf clover has order-four rotation or 4-fold rotation; it is tertrameric/tertramerous. The red arrow shows how many degrees the half-leaf needs to turn to exactly match the next: two times 45°.
Radial Symmetry in Nature
In nature, radial symmetry abounds – although it is nowhere near as common as bilateral symmetry. The most visible examples of radial symmetry in nature are actinomorphic flowers. The shape of a flower is not at all random. While color and scent can provide other means of attraction, actinomorphism gives a flower the greatest chance of pollination by multiple species. If we think of flowers that only attract one type of pollinator, such as the bee orchid, they are more likely to exhibit bilateral symmetry (zygomorphism). The bee orchid mimics the form of a female bee and so encourages males of that species to try to mate with it and in doing so, pollinate the flower. Bees are also the primary pollinators of monkshood or Aconitum flowers. These flowers are also zygomorphic.

Radial symmetry means that more insect types can land on the flower, drink the nectar, and unwittingly transport pollen to other flowers of the same species. The shape of a multi-fold form is recognized as a food source. Together with color, blooming time, and scent, the shape of the flower is a survival mechanism that increases its chances of reproduction.
Once a flower has been pollinated, the plant can produce seeds. Some of these seeds are enclosed in pods, others within fruit. Slice through the center of most fruits and you will see some beautiful examples of radial symmetry. The segments of an orange, the seed distribution of a kiwi fruit, and the five-pointed star of an apple core, for example.
Radial symmetry, or at least approximate radial symmetry, increases the strength of spider webs, evenly distributing the force of impact when a large insect becomes trapped. Using radial threads and spiral threads, these multi-fold structures certainly look like viable rotational symmetry examples.
Tiny crystals of ice in the form of snowflakes show spectacular radial symmetry. In China, in 135 B.C., Han Yin wrote down his observations. He reported that the flowers of plants are usually five-pointed, and ‘snow flowers’ six-pointed. When, in 1885, Wilson Bentley took the first photographs of snowflakes – 5,000 of them – he told us what is now accepted as fact, that no two snowflakes are alike.

Organisms with Radial Symmetry
A radially symmetrical organism has a top and a bottom called the oral and aboral side respectively and not the head or rear. It is impossible to distinguish a left or right side.
Does an octopus have radial symmetry? Only if it is sitting flat on a piece of glass and you can’t see its head. If so, the eight suckered tentacles radiate from a central point. The rather lopsided head means that even when looking down onto an octopus, you won’t see any sign of radial symmetry, although many cartoon octopi ignore this fact.
The majority of organisms that exhibit radial symmetry are found in the ocean. As has already been mentioned right at the start of this article, one of the criteria for radial symmetry is that each repeated section is exposed to the same environment.
Marine and freshwater organisms with radial symmetry rarely move at speed. Some stick to rocks and use radially-symmetrical filamented heads to catch microorganisms or small fish. Some use radial tentacles to creep along the ocean floor or float along the current. But the environment that surrounds each repeated shape is the same – water.

Organisms with radial symmetry are usually very simple. The primary phyla and classes are:
- Phylum Cnidaria: Hydrozoa, Scyphozoa, Cubozoa, and Anthozoa
- Phylum Myxozoa: Myxosporea
- Phylum Ctenophora: Tetaculata, and Nuda
Examples of radial symmetry animals most commonly list members of these phyla. Cnidaria is a group of marine and freshwater organisms that either take on the form of a stationary polyp or the moving form of a medusa. Polyps in the group Anthozoa include sea anemones and corals. Hydrozoa, Scyphozoa, and Cubozoa are medusa in form and include all forms of jellyfish. The life cycle of Cnidaria is often a mix of larva and/or polyp or medusa. For example, a jellyfish larva settles in a safe place and becomes a bilaterally symmetrical polyp. When mature, the polyp buds to become multiple young medusae or jellyfish with radial symmetry.

Phylum Myxozoa should, anatomically-speaking, be part of phylum Cnidaria but these parasites are often given their own category. These extremely tiny, radially-symmetric organisms cannot survive without two aquatic hosts, one of which is nearly always a fish.
Phylum Ctenophora or comb jellies have sticky cells on their tentacles to catch their prey. They are actually biradial in form, and their symmetry is three dimensional and a mix of radial and bilateral symmetry.
As with jellyfish, animals can develop different body symmetry according to their life cycle. For example, the sand dollar starts life as a bilaterally-symmetric nymph and exhibits rotational symmetry as an adult (see below). If radially-symmetric organisms began life in a bilaterally-symmetric form, they are said to exhibit secondary radial symmetry.

It is not only the form of an organism or plant that has radial symmetry but also certain internal structures. These include tubules and eyes. If you look at a cross-section of the human intestine, it is radially symmetrical; a circle is radial symmetry perfection in mathematical terms – no matter how many times you divide it from the center outwards (except when using a single line), each section will be exactly the same in form. If you have ever looked at or colored in a mandala, you will have noticed how the same pattern repeats within the circle. The human brain and the brains of many animals are wired to appreciate symmetry. In fact, our eyes detect 5-fold radial symmetry (and above) at a greater speed than with objects possessing bilateral symmetry.
In the world of viruses, radial symmetry can also be found. Examples are the rotavirus and norovirus. Even their surface proteins are arranged at similar distances from each other.
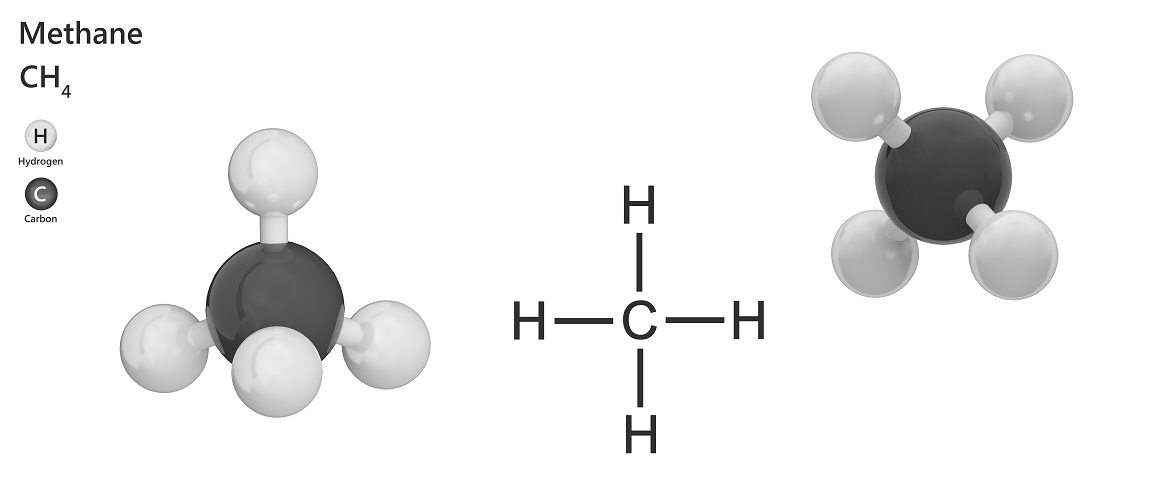
Some molecules also exhibit this type of symmetry, for example methane. The central carbon atom bonds with four hydrogen atoms. If lines are drawn through the carbon atom and either to the side or through the middle of the hydrogen atoms, if you rotate each section they will match each other after 90° – 4-fold radial symmetry.
Radial Symmetry and Movement
When humans and other mammals move, they can do so quickly. Bilateral symmetry creates balance and helps us to propel ourselves forward. This is not the case with radial symmetry. Organisms that exhibit radial symmetry often depend on the environment to move them, such as the ocean currents or the wind. Others are immobile, either stuck to a rock under the sea or attached to the ground as plants. If a radially symmetrical animal has to move from one place to another it rarely moves from side-to-side; instead it moves up and down in the direction of oral or aboral end. When these organisms do move to the side, they seem to use the same mechanisms as organisms with bilateral symmetry.
One study on brittle stars showed that these marine organisms travel in different horizontal directions by extending one of five jointed tentacles. The two tentacles to either side then grab the sand or rock and pull the brittle star forward. The central tentacle acts as a central plane and the two others are mirrored in it, just as with bilateral symmetry. Bilateral symmetry means forward motion; without this technique the brittle star would move vertically. Whenever the brittle star wants to change direction, it simply uses another tentacle as the central plane.

Radial Symmetry vs Bilateral Symmetry
Radial versus bilateral symmetry is easy to explain. Bilateral is two-sided symmetry and the most common form – 90% of organisms and plants are bilaterally symmetrical. An anteroposterior plane that cuts vertically through the center of the head, chest, abdomen and pelvis of a human will split it into two near-exact parts that are mirror images of each other.
Animals that are shaped according to bilateral symmetry have a top (dorsal) side and bottom (ventral) side, a head (anterior) and tail (posterior), and a left and right side. Examples of bilateral symmetry in the animal world include worms and snails, lobsters, cats, seals, turtles, and humans.

All you need to do is image a line through its middle – if the shape either side is a mirror image of the other, the organism, plant, molecule, microorganism, house, window, anything at all, is bilaterally symmetrical. Higher life forms with bilateral symmetry have developed to move forwards very quickly. Our eyes and noses face forwards and our muscles propel us forwards (how quickly can you run backwards?). We can quickly sense what is coming and react.
If you can draw more than one line through the center of a picture or imagined image of an organism, pattern, or even a part of the body, and when each section looks the same and can be rotated to match the section that comes before or after it, you will have discovered that it is radially symmetrical. There are no mirror images in radial symmetry. Just repeated shapes through two or more planes.

Examples or radial symmetry in animals and organisms have been given throughout this article. Remember, these organisms do not have anterior and posterior sides, right or left sides, or dorsal and ventral surfaces. Instead, they have a mouth (oral) and base (aboral) side. Our eyes automatically pick up on rotational symmetry examples, so all you need is a little faith in your gut instinct.
Quiz
